On Binary Integer Subtraction with the x86 SUB Instruction
By Yue LI on 04 May 2023
The x86 instruction set has a basic instruction SUB for subtraction of signed or unsigned integers. This blog post is to clarify certain questions about the SUB instruction, as follows.
How is it possible to do both signed and unsigned subtraction, using only one instruction? In other words, what is the relation between signed and unsigned subtraction?
How often does signed subtraction overflow happen?
Why does the conditional jump instruction JGE test the equation OF=SF (i.e., that the overflow flag OF equals the sign flag SF) for a greater-than-or-equal relation between two signed integers ?
1. Two's Complement Interpretation
Given a sequence of bits, it is natural to interpret it as a binary unsigned integer. Then we have (unsigned) addition and subtraction defined for the bit sequences in the usual way. The CF (carry flag) is set if there is a carry (for addition) or a borrow (for subtraction).
Two's complement is a way to interpret an unsigned integer as encoding a signed integer. The name "two's complement" is historical and may not make sense in the modern context (see my earlier blog explaining the name "two's compliment").
However, two's compliment is convenient since it does not require anything more special to do addition and subtraction for signed integers than those algorithms for unsigned integers. We shall see that unsigned integer subtraction results are often reusable and are actually reused as results of signed subtraction.
2. Signed Subtraction is just Unsigned Subtraction
Let us now draw a table by hand on a piece of paper (I'm reusing kids' sketch paper), for unsigned binary integer subtraction, and then look at the bits in the table as if they are two's compliment encoding of signed integers, and see how much sense it makes. For simplicity, but without loss of generality, we work with unsigned integers of 3-bit long.

In the table, I compute X minus Y by regarding X and Y as unsigned integers. The table has 8 columns and 8 rows, filled firstly using a thin black pen with the possible values of X and Y and the results of their unsigned subtraction.
Next I use a green highlighter to mark the lower left corners of those cells that have the CF (carry flag) set - these are results obtained when Y is above (i.e. larger than) X (both are interpreted as unsigned integers). I also intended to use an orange highlighter to mark the upper right corners of those cells that has the OF (overflow flag) set, but this is impossible before interpreting the cells as two's complement signed integers. So I instead use an orange highlighter to write down in each cell the corresponding two's complement interpretation in decimal, and assess which of the results are still correct and which are not, and I use a pink highlighter to circle all the incorrect (overflow) results.
Overflow happens when the true result is outside the range of signed integers representable under a given bit length. For 3-bit signed integers, this range is from -4 (minus four) to 3. I make a mistake when circling the cells, and draw short thin strikes on the wrong circle.
We observe that although the table is for unsigned integer subtraction, most (those that are not in pink circles) of the results still make sense when the bits are reinterpreted as two's compliment signed integers. Hence we get our first question answered: to do subtraction for two's complement signed integers, just do subtraction as if the bits denote unsigned integers.
Although the results are not always correct (overflow gives incorrect results), at least overflow is signalled by the OF, and after all, even unsigned subtraction may have truncated results (when CF is set). We have seen that about half of the unsigned subtraction results have CF set. We now ask how much of signed subtraction has OF set?
3. A Quarter of Signed Subtraction Overflows
I want to exercise my table drawing skill with longer bit sequences. If every sequence is 1cm long, my notebook allows me to list 32 of them in a row. So I draw a new 32 times 32 table for subtraction of unsigned 5-bit integers.
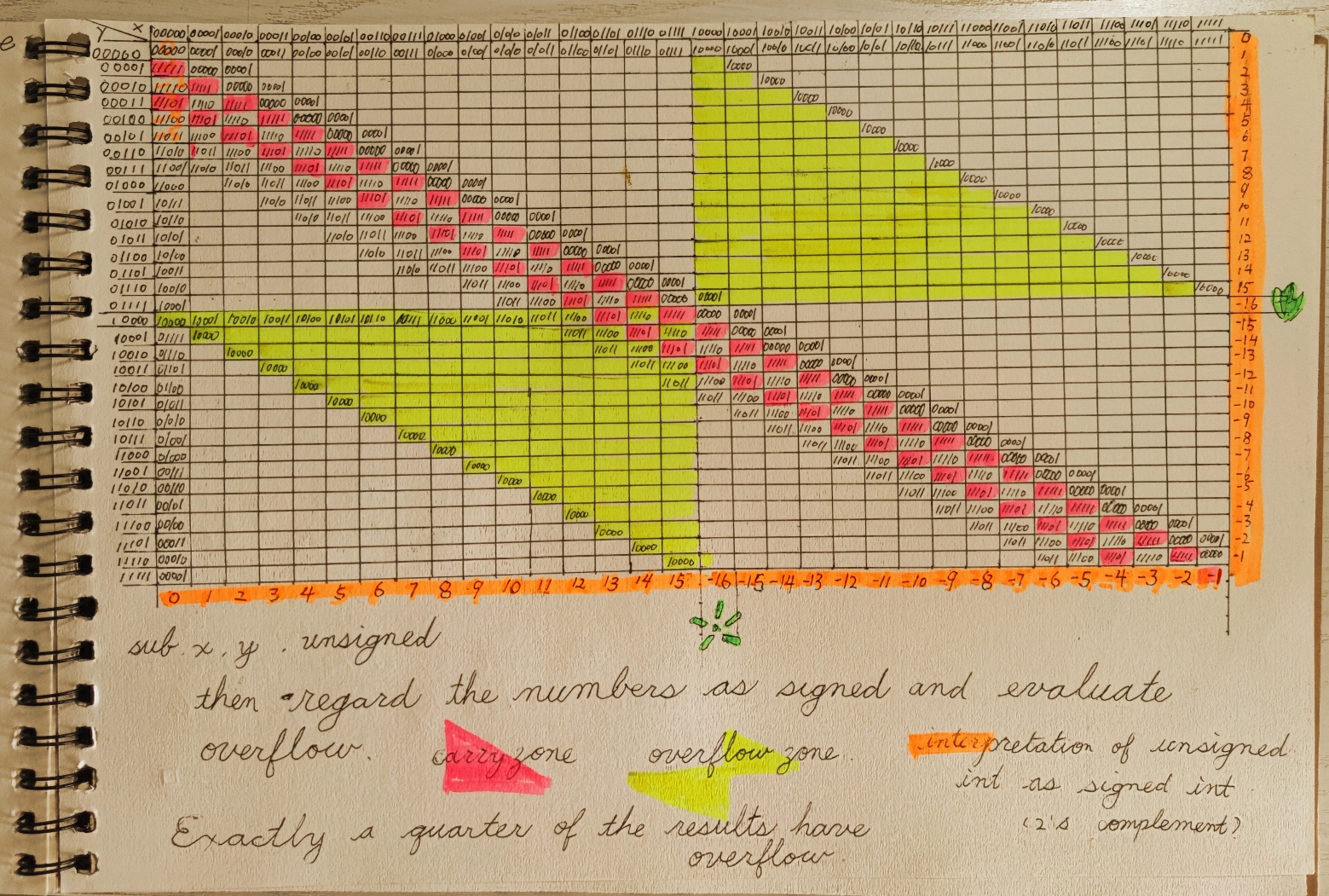
I get lazy when I find there are too many cells to fill. However, I discover laws that render the table logically structured, so the entries become predictable.
Firstly, the leftmost column is easy to fill, for it is subtracting from zero, or sign reversing. The top row is also trivial, for it is subtracting zero. After that, the main diagonal from top left to bottom right can be uniformly filled with zeros. What is important is that each minor diagonal that is parallel to the main diagonal can be filled uniformly, and numbers from neighbouring diagonals differ by 1. For this reason we can easily determine the number in a given cell by tracing the diagonal that contains it towards the top-left end, which resides in either the leftmost column or the top row, which we already easily filled. I use pink colour to highlight two diagonals.
There are two diagonals, and one column and one row, which are special and all of which correspond to the bits 10000. We shall call them collectively as the min-negative borders, for 10000 represents the smallest negative integer under two's complement interpretation. The overflow zone is exactly the bow-tie shaped area, highlighted in yellow, enclosed by the min-negative borders. The area of the overflow zone is exactly a quarter of the entire table if you imagine that you cut off the two triangular components of the zone and align their sloping edges to make a rectangle, which is a quarter of the table.
Now we have an idea of how often overflow of signed subtraction happens - we start from an unsigned subtraction table, then we reinterpret the bits, and mark the overflow zone, and finally conclude that it is a quarter of the entire table. Other places in the table are correct signed subtractions.
4. The OF=SF Equation for Signed Integer Comparison
The SUB instruction modifies the OF (overflow flag) and the SF (sign flag). The JGE conditional jump instruction performs a jump if the two signed integers in a prior subtraction has the greater-than-or-equal relation, and this is verified by checking the equation OF=SF. We now prove that OF=SF after SUB X, Y if and only if X is greater than or equal to Y. Again we work with a small bit length. This time we not only highlight the overflow zone but also mark the SF-set zone (orange left cell border), and the less-than zone (green right cell border).
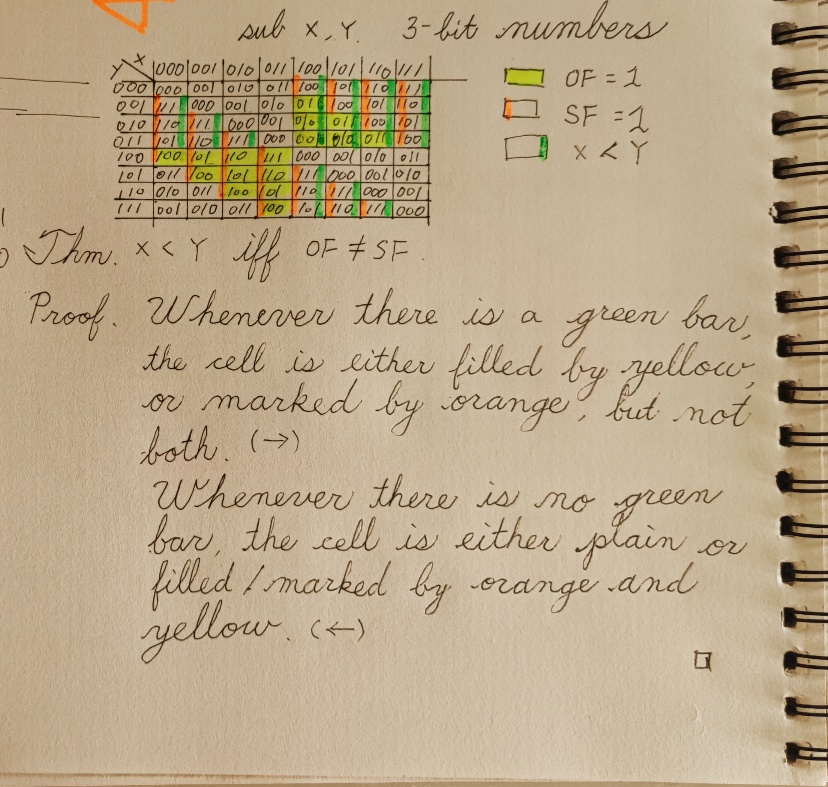
It is clear that whenever a cell has green mark (for less-than relation between X and Y), it has exactly one of the OF and SF marks (meaning OF≠SF); otherwise if a cell has no green mark (for greater-than-or-equal), either it has both, or it has none of the OF and SF marks (meaning OF=SF).